R z gwiazdką: alternatywna metoda szacowania „gwiazdy przewodniej” polityki pieniężnej
Naturalna (neutralna) stopa procentowa to realna stopa procentowa, przy której wzrost gospodarczy pozostaje na poziomie potencjału, a inflacja na poziomie celu. Nasz artykuł proponuje nowe podejście do szacunków naturalnej stopy procentowej, oparte na modelu, w którym bank centralny minimalizuje straty spowodowane inflacją i odchyleniami produkcji od potencjału.
Zarówno w Stanach Zjednoczonych, jak i strefie euro szacunki naturalnej stopy procentowej świadczą o okresie łagodnej polityki pieniężnej zakończonym globalnym kryzysem finansowym, w następstwie którego nastąpiło gwałtowne zaostrzenie. Co więcej, przynajmniej od 1987 r. wersja reguły Taylora oparta o naturalną stopę procentową dobrze sprawdza się w wyjaśnianiu polityki pieniężnej w USA.
Naturalna stopa procentowa – czyli „r” z gwiazdką – należy do najważniejszych pojęć polityki pieniężnej, bo wyznacza kurs dla polityki bankowców centralnych w zakresie stóp procentowych (Powell 2018). To wprowadzone przez Wicksella (1898) pojęcie odnosi się do hipotetycznego poziomu stóp procentowych, przy którym wzrost gospodarczy postępuje w tempie wzrostu produktu potencjalnego, a inflacja pozostaje na poziomie celu. Ponieważ naturalna stopa procentowa jest nieobserwowalna, trzeba ją szacować.
Jednym z najczęściej stosowanych przybliżeń r* jest oszacowanie Laubacha i Williamsa (2003). Niedawne wznowienie publikacji tego oszacowania po dwuletniej przerwie spowodowanej wstrząsem COVID-19 (Holston et al. 2023) zapoczątkowało gorącą debatę w mediach społecznościowych na temat jego użyteczności. Nie tylko bowiem tej – jednej z najważniejszych – wartości referencyjnych w polityce pieniężnej zabrakło właśnie wtedy, kiedy silny wstrząs podwyższył znacznie poziom niepewności, to jeszcze zmiany w procedurze szacowania zmieniły cały szereg czasowy wstecz do lat 1960, w niektórych przypadkach w istotnym stopniu.
To najnowsze zastrzeżenie wpisuje się w krytykę przedstawianą w dotychczasowej literaturze przedmiotu, w której zgłaszano różne zarzuty wobec szacowania naturalnej stopy procentowej. Dotyczy ona m.in. silnej i stałej tendencji zniżkowej obserwowanej od lat 60. Buncic (2021) wykazuje, że za tę tendencję odpowiada przede wszystkim składnik losowy modeli autoregresyjnych, którego włączenie do opisu cechują z punktu widzenia ekonometrii istotne wady. Konsekwentny trend zniżkowy wynika również po części z wysokich wartości r* w latach 60., uwzględnianych tylko w oszacowaniu Laubacha i Williamsa (2003) oraz Holstona i in. (2017), ale nie w większości innych oszacowań.
Inny element krytyki pracy Laubacha i Williamsa dotyczy oszacowań luki popytowej. Przed nastaniem kryzysów finansowych, szacunki te w istotnym stopniu pokrywały się z szacunkami Biura Budżetowego Kongresu. Jednak od ich wybuchu pomiędzy obydwoma szeregami danych pojawiła się luka sięgająca nawet siedmiu punktów procentowych.
Chociaż Laubach i Williams opisują teoretyczny sposób określania naturalnej stopy procentowej w ramach prostego modelu keynesowskiego, oszacowanie przeprowadzają w oparciu o stan opisany przez złotą regułę w standardowym neoklasycznym modelu wzrostu, czyli w zupełnie innych ramach teoretycznych. W niedawnej pracy (Bofinger i Haas 2023) przedstawiamy podejście pozwalające oszacować naturalną stopę procentową na podstawie modelu keynesowskiego opisanego przez Laubacha i Williamsa. Wykorzystujemy prosty nowokeynesowski model makroekonomiczny, w którym bank centralny ustala stopy procentowe w sposób minimalizujący lukę popytową y oraz odchylenie stopy inflacji π od wartości docelowej. Tak więc bank centralny kieruje się funkcją straty uwzględniającą lukę inflacyjną i popytową. Ponieważ cele są symetryczne, obydwa wyrażenia podniesiono do kwadratu, parametr preferencji waży zaś względne znaczenie obydwu wyrażeń.
Stosując taką funkcję strat, możemy wyodrębnić okresy neutralne, tzn. takie, w których całkowita strata równa się zeru. Zakładając, że świadczy to o braku szoków egzogenicznych, można wyprowadzić wartość zastępczą dla naturalnej stopy procentowej w tych okresach. Przyjmujemy, że w takich neutralnych okresach faktyczna realna stopa procentowa banku centralnego bliska jest stopie naturalnej. Na podstawie tych obserwowalnych przejawów stopy naturalnej, obliczamy średnią kroczącą, aby wygładzić dostosowania pomiędzy różnymi odczytami parametru. W okresach „nieneutralnych” z kolei nie można zaobserwować oznak stopy naturalnej, dlatego też podstawiamy ostatnią wartość z uśrednionych szeregów czasowych.
Obliczona funkcja straty dla gospodarki USA dobrze odzwierciedla ewolucję gospodarki USA w okresie ostatnich 70 lat. Lata 60. cechowały się pewną stabilizacją i niską inflacją. Po nich nastąpił okres wysokiej inflacji w latach 70. i na początku lat 80. oraz reakcja Fedu pod przewodnictwem Volckera, która doprowadziła do jej spadku – ale też do recesji. Następnie obserwujemy okres „wielkiego umiarkowania” (great moderation), gdy strata była niska, potem kryzysy finansowe z ich w zasadzie permanentnymi stratami oraz recesję spowodowaną przez COVID-19, po której pojawiły się wysokie stopy inflacji.
Jeśli uwzględnimy jeszcze realne oprocentowanie funduszy federalnych i określimy okresy neutralne jako te, w których funkcja straty przyjmuje wartości nie większe niż 5, możemy bezpośrednio odczytać wartości zdefiniowanej przez nas miary naturalnej stopy procentowej w odpowiednich okresach
Jak opisano powyżej, obliczamy średnią kroczącą obserwowanych wartości naturalnej stopy procentowej w celu uwzględnienia faktu, że jest to zjawisko o charakterze średnio- lub długoterminowym. Stopa naturalna może być wykorzystana do oceny kursu polityki pieniężnej. Wykres poniższy pokazuje naturalną stopę procentową dla Stanów Zjednoczonych (panel górny) i strefy euro (panel dolny) oraz odpowiednie realne stopy procentowe banku centralnego.
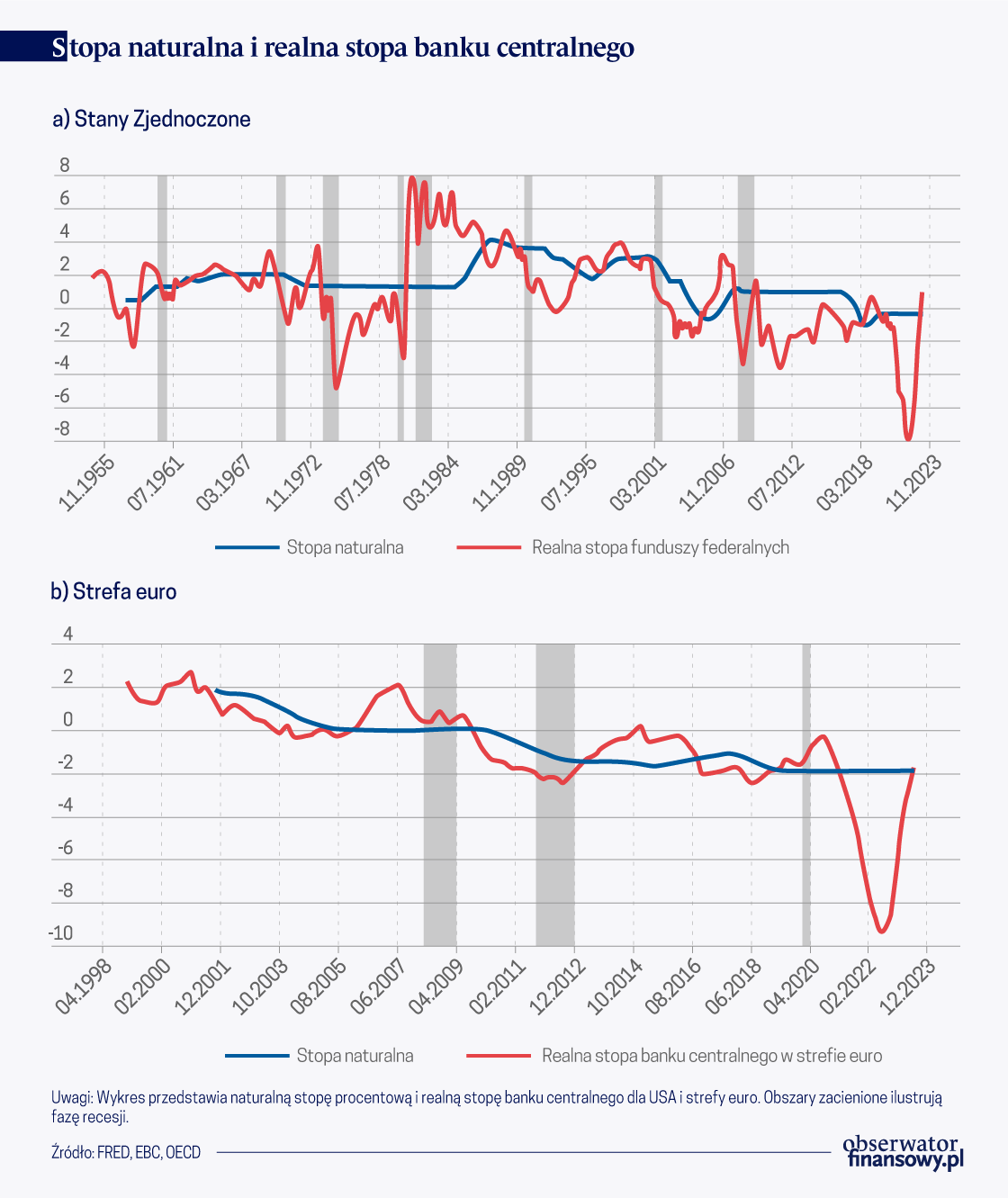
Wykres 1.Stopa naturalna i realna stopa banku centralnego
W obydwu przypadkach stwierdzamy dłuższe okresy łagodnej polityki pieniężnej w latach poprzedzających kryzys finansowy, po których następowało gwałtowne zacieśnienie polityki pieniężnej tuż przed wybuchem kryzysu. Nasza miara stopy naturalnej jest też niewrażliwa na gwałtowną, ale krótkotrwałą recesję COVID-19, co sugeruje, że jak na razie wygląda ona raczej na przejściowy szok.
Nasza miara naturalnej stopy procentowej wykazuje zastanawiającą zbieżność z wieloma innymi szacunkami naturalnej stopy procentowej. Obliczenia wskazują na wysoką niepewność oszacowań r* – przedziały ufności wynoszą do dwóch punktów procentowych od mediany lub wartości średniej oszacowań. Nasza miara stopy naturalnej często mieści się w granicach przedziałów ufności innych miar, co wskazuje, że te oszacowania są statystycznie nie do odróżnienia. Zgodnie z wszystkimi innymi miarami, z wyjątkiem Laubacha i Wlliamsa (2003) oraz Holstona i in. (2023), nie znajdujemy potwierdzenia długookresowego spadku naturalnej stopy procentowej. Jest to również zgodne z danymi empirycznymi dotyczącymi zwrotu netto z kapitału netto w najbardziej rozwiniętych gospodarkach.
Na koniec, szacujemy regułę Taylora z uwzględnieniem naszej stopy naturalnej w celu sprawdzenia przydatności naszej miary stopy naturalnej w heurystyce polityki pieniężnej. Wykres poniższy pokazuje „stopy Taylora” dla USA i strefy euro na tle realnych stóp banku centralnego.
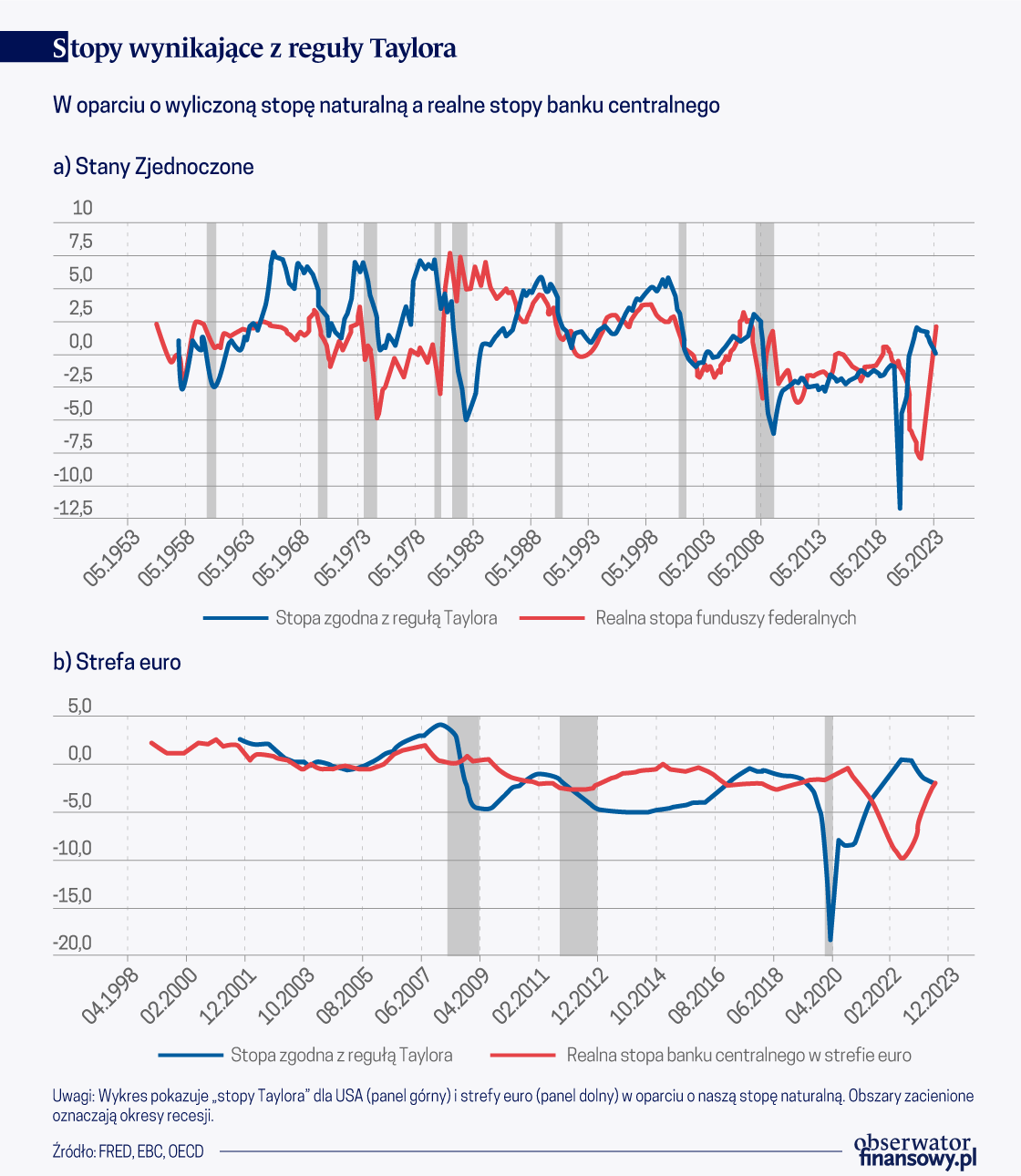
Wykres 2. Stopy wynikające z reguły Taylora
Górny panel wykresu pokazuje, że nasza „stopa Taylora” jest w istocie bardzo zbliżona do rzeczywistej realnej stopy funduszy federalnych od roku 1987. To zresztą w latach 1987-1992 Taylor (1993) sformułował swoją słynną regułę. Odchylenia w późnych latach sześćdziesiątych i siedemdziesiątych, kiedy faktyczna realna stopa funduszy federalnych była znacznie niższa od „stopy Taylora”, pociągnęły za sobą wysoką inflację. Z kolei we wczesnych latach 80. „stopa Taylora” utrzymywała się znacznie poniżej realnej stopy funduszy federalnych, co wskazuje na zbyt restrykcyjny charakter ówczesnej polityki pieniężnej. Okres poprzedzający kryzys kredytów hipotecznych również wykazuje odchylenia od reguły Taylora, sygnalizując nadmiernie ekspansywną politykę pieniężną. Podobne odchylenia stwierdzamy w odniesieniu do strefy euro w okresie poprzedzającym kryzys finansowy. W okresie kryzysu euro i w kolejnych latach stwierdzamy zbyt restrykcyjną politykę pieniężną, która mogła przyczynić się do hamowania ożywienia gospodarczego.
Pomimo swojej prostoty, nasza metodologia opiera się na konsekwentnych teoretycznych odniesieniach do prostego modelu nowokeynesowskiego i zasadniczo pozostaje w zgodzie z obecnymi metodami wyznaczania r*. Biorąc pod uwagę czysto teoretyczny charakter tego pojęcia oraz fakt, że wszystkie metody jego pomiaru obarczone są bardzo wysoką niepewnością – o czym świadczą przedziały ufności o zakresie do sześciu punktów procentowych – proste obliczenia mają swoje zalety.
—
Peter Bofinger – Profesor Katedry polityki pieniężnej i ekonomii międzynarodowej Uniwersytetu w Würzburgu
Thomas Haas – Doktorant na Uniwersytecie w Würzburgu
Artykuł ukazał się w wersji oryginalnej na platformie VoxEU, tam też dostępne są przypisy i bibliografia.
W latach 90. XX w. wydawało się, że patent na prowadzenie polityki pieniężnej jest znany. Kraje małe, o otwartej gospodarce i swobodnych przepływach finansowych, powinny zrezygnować z prowadzenia własnej polityki monetarnej i przywiązać kurs swojego pieniądza do zagranicznej waluty dominującej w obrotach handlu zagranicznego. Oczywiście takie rozwiązanie wymagało prowadzenia odpowiedzialnej polityki budżetowej i zaufania rynków finansowych wykluczające raptowny odpływ zagranicznego finansowania.
Z powodu gwałtownego wzrostu inflacji banki centralne ponownie znalazły się w centrum uwagi debaty publicznej Autorzy proponują nowatorską metodę identyfikowania egzogenicznych zmian w polityce pieniężnej na podstawie doświadczeń Fed.
Ważną częścią kanału stopy procentowej w mechanizmie transmisji polityki pieniężnej są dostosowania stóp kredytowych i depozytowych w bankach komercyjnych do zmian podstawowej stopy procentowej banku centralnego.
Historia pokazuje, że naród, który odzyskuje wolność i zdobywa panowanie na terytorium swojego państwa bagnetem żołnierza, nie zapewnia sobie tym samym zupełnej suwerenności. Dopiero odzyskanie władzy nad walutą narodową albo stworzenie tej waluty, staje się prawnym imperatywem suwerenności i fundamentem stabilnej gospodarki narodowej.
W ciągu najbliższych 30 lat rynek pracy będzie podlegał rozmaitym trendom. Do najważniejszych należą rozwój sztucznej inteligencji, starzenie się społeczeństw i ekologiczna transformacja. Każdy z nich będzie się wiązał z nowymi zagrożeniami, ale też i zawodowymi szansami.
W ciągu ostatnich 200 lat bankowość centralna przeszła poważną ewolucję, zmieniały się jej zadania oraz reguły polityki pieniężnej. Tekst pokazuje z tej perspektywy dwa banki centralne: Bank Polski (1828–1866) oraz Bank Polski SA (1924–1939). Akcent położono na okoliczności ich powstania oraz intencje i oczekiwania projektodawców, które zdeterminowały statutowy zakres ich uprawnień. Pokazano trudne wybory odnośnie do priorytetów i gradacji celów, przed jakimi stawiała je rzeczywistość gospodarcza. Okoliczności te skłaniały do pytań o właściwe cele i zasady funkcjonowania banków centralnych, tworzyły przestrzeń dla ścierania się koncepcji swoistego bankowego wariabilizmu i statyzmu.
Porządek z Bretton Woods upada, epoka Potęgi Pieniądza jest w odwrocie i nic tego nie zmieni, a na horyzoncie widać świt multipolarnego świata – przekonuje dr Fadi Lama, doradca EBOR, w książce „Why The West Can't Win: From Bretton Woods to a Multipolar World”.
Pierwszym prezesem Banku Polskiego SA został Stanisław Karpiński - wybitny ekonomista, bankowiec i minister skarbu. Jako teoretyk i praktyk cieszył się niekwestionowanym autorytetem zarówno w środowisku bankowym, jak i politycznym.
„Najwyższym dobrem naszym jest nasza państwowość, którą musimy postawić na wysokim poziomie i zabezpieczyć jej całkowitą niezależność. Dla dobra tej naszej państwowości musimy dawać wszystko, co tylko jest w naszej mocy. […] Podstawą zdrowego rozwoju życia gospodarczego oraz siły finansowej państwa jest zdrowa i silna waluta. W celu jej stworzenia i zachowania musi całe społeczeństwo ponosić znaczne ofiary” – o tych słowach, skreślonych przez Władysława Grabskiego, powinien pamiętać każdy polityk, któremu dobro Polski leży na sercu. Wszyscy muszą o tym pamiętać, bo w tych kilku zdaniach zarysowany został cel i zobowiązanie, do realizacji których powinniśmy dążyć jako ludzie wolni i ceniący swoją wolność.
Najnowsze wydanie „Obserwatora Finansowego” ukazuje nam wizje przyszłości bliskiej i dalekiej. W tym numerze, najlepsi eksperci postarają się odpowiedzieć na kilka kluczowych pytań, dotyczących sztucznej inteligencji i tego jak generatywna AI wpłynie na bankowość, edukację oraz inne dziedziny naszego życia.
ChatGPT zapoczątkował nowy etap automatyzacji. W nadchodzących latach generatywna sztuczna inteligencja może doprowadzić do głębokich zmian na rynku pracy oraz znacząco przyspieszyć wzrost gospodarczy.
Historia pokazuje, że naród, który odzyskuje wolność i zdobywa panowanie na terytorium swojego państwa bagnetem żołnierza, nie zapewnia sobie tym samym zupełnej suwerenności. Dopiero odzyskanie władzy nad walutą narodową albo stworzenie tej waluty, staje się prawnym imperatywem suwerenności i fundamentem stabilnej gospodarki narodowej.
Sztuczna inteligencja powoli zmienia sposób działania banków i instytucji finansowych. Pomaga im zredukować ciężar biurokracji, ale także podejmować szybsze decyzje oraz utrzymywać efektywny kontakt z klientami. A będzie jeszcze lepiej. W perspektywie czeka kilkunastoprocentowy wzrost EBITDA.
Budowa Centralnego Portu Komunikacyjnego wzmocniłaby znacznie pozycję Polski w europejskiej gospodarce – stwierdził w rozmowie z „Obserwatorem Finansowym" dr Andreas Wittmer, dyrektor zarządzający Centrum Badań Lotniczych na Uniwersytecie w St. Gallen.
Współczesne problemy prawne Unii Europejskiej, sztuczna inteligencja w bankowości oraz polityka pieniężna były tematami grudniowego zjazdu na podyplomowych studiach MBA organizowanych w ramach drugiej edycji projektu „Akademia NBP”.
Portal ekonomiczny NBP „Obserwator Finansowy” ponownie znalazł się w czołówce najbardziej opiniotwórczych mediów w kategorii „Media ekonomiczne i biznesowe”, wyprzedzając m.in. „Parkiet”. Wzrost cytowalności treści publikowanych na łamach serwisu wzrósł w kwietniu w odniesieniu do marca 2023 r. o 37 proc.
Sytuacja gospodarcza w Polsce na tle innych krajów przedstawia się korzystnie. Warto zauważyć, że w szybkim tempie nadrabiamy dystans dzielący Polskę od poziomu życia w wybranych państwach europejskich. W ciągu ostatnich czterech lat dynamika wzrostu PKB plasowała Polskę powyżej innych krajów europejskich, zarówno strefy euro, w tym Niemiec i Francji, jak i krajów Unii Europejskiej z własną walutą, np. Czech.
Większość polskich przedsiębiorców odczuła skutki wojny w Ukrainie, choć jej wpływ oceniają w zróżnicowany sposób – wynika z badania przeprowadzonego przez Polski Instytut Ekonomiczny.
W styczniu 2020 roku Wielka Brytania formalnie opuściła Unię Europejską. Oczekiwane korzyści z brexitu, poza odzyskaniem suwerenności w zakresie kształtowania prawa i zewnętrznych relacji gospodarczych, jednak się nie zmaterializowały. Widoczny jest natomiast spadek wydajności i konkurencyjności brytyjskiej gospodarki, co wpływa także na kondycję rynku pracy.
