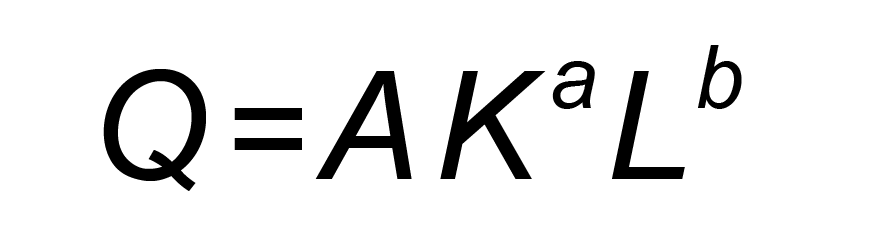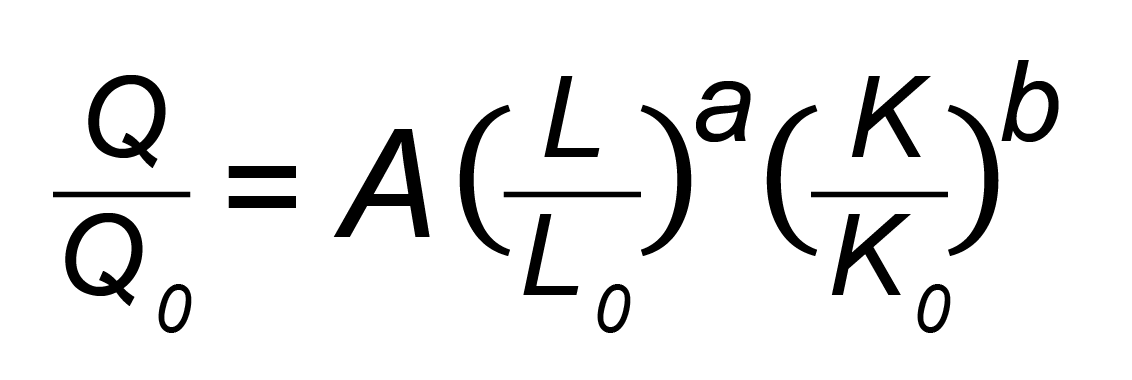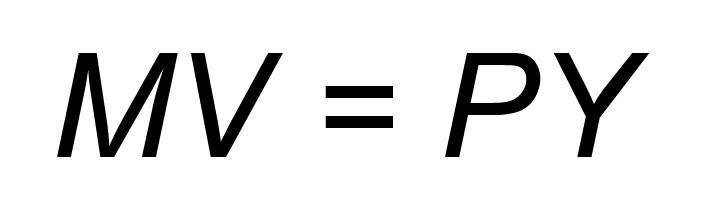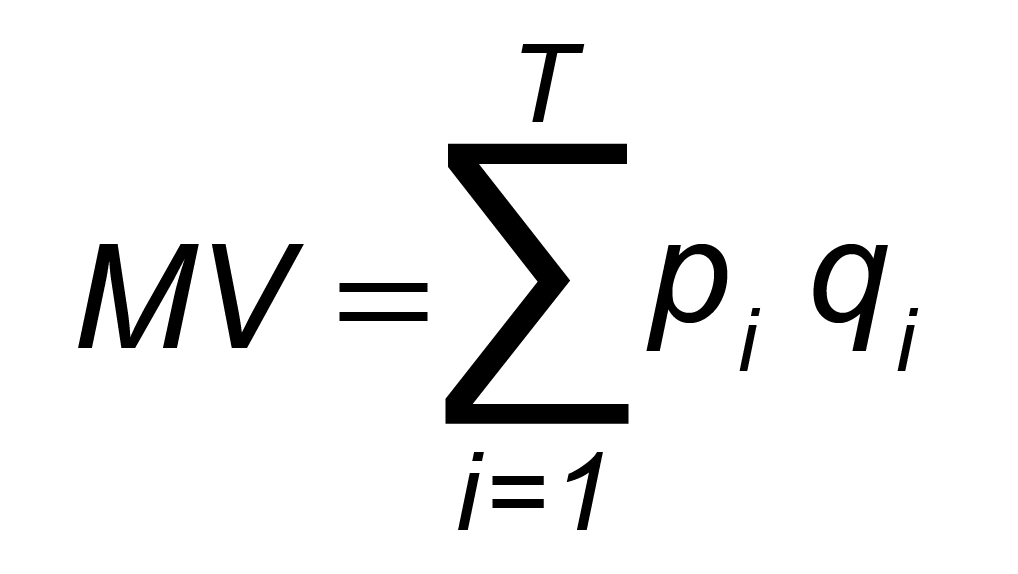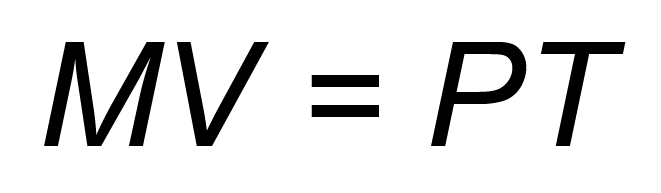Suwerenna waluta, suwerenny naród
Kategoria: Trendy gospodarcze
Pracował w Instytucie Nauk Ekonomicznych na Wydziale Prawa, Administracji i Ekonomii Uniwersytetu Wrocławskiego.

(©Envato)
Wybrałem cztery takie zagadnienia: problemy związane z rozumieniem podaży i popytu (krzywej podaży i krzywej popytu), funkcję produkcji Cobba-Douglasa, równanie wymiany Fishera (stosowane w ilościowej teorii pieniądza) oraz powszechnie używaną przez ekonomistów krzywą Phillipsa.
Czego natomiast nie znajdziemy w podręcznikach i w tym artykule? – takie najważniejsze zagadnienia, których nie znajdziemy np. w najpopularniejszych podręcznikach ekonomii Paula Samuelsona czy Gregory Mankiw, to zaakceptowanie, że nie ma czegoś takiego jak obiektywna, powszechnie uznawana wartość ekonomiczna i uznanie, że wartość ekonomiczna jest zawsze subiektywna. Ta subiektywność wartości ekonomicznej związana jest z kolejnym niedyskutowanym w podręcznikach zagadnieniem, mianowicie tym, że tylko jednostki działają, dokonują wyboru i podejmują decyzje. Nie dyskutuje się w tych podręcznikach różnicy pomiędzy ceną a wartością ekonomiczną, wręcz uznaje się, że cena jest miarą wartości ekonomicznej. Nie wspomina się o tym, że „rynek nie jest grą o sumie zerowej”. Nie przedstawia się w tych podręcznikach „problemu wiedzy” (choćby w kontekście koncepcji Friedricha von Hayeka i Michaela Polanyi), nie uczula się studentów, żeby zwracać uwagę na to, że należy uwzględniać w rozważaniach ekonomicznych nie tylko, „co jest widoczne”, ale przede wszystkim to, co „nie jest widoczne” (tutaj kłaniają się Frédéric Bastiat i Henry Hazlitt), czy o ogromnej roli przedsiębiorcy i przedsiębiorczości w rozwoju gospodarczym (poczynając od idei św. Bernardyna ze Sieny, przez Richarda Cantillona, Jean-Baptiste Say’a, Josepha A. Schumpetera, Israela Kirznera). O ułomnościach ortodoksyjnych podręczników można byłoby długo pisać. Zostawię to jednak na inny artykuł.
Większość ekonomistów głównego nurtu nie widzi różnicy pomiędzy takimi pojęciami jak popyt a funkcja popytu (czy krzywa popytu). Widać to w podręcznikach do nauki ekonomii, gdzie często możemy przeczytać frazy typu „Popyt na dobro przedstawiono na rysunku…”. Zamiast poprawnego „Krzywą popytu na dobro przedstawiono na rysunku…”. Ekonomiści nieortodoksyjni (nawet nie muszę odwoływać się tutaj do bliskich mi ideowo ekonomistów ze szkoły austriackiej) są świadomi tej różnicy. Niech jako przykład posłuży Zygmunt Heryng, który w opublikowanej ponad 120 lat temu Logice ekonomii napisał: „W popycie jak i w podaży wyraża się uświadomiona dążność do ciągłego uzupełniania naszej energii społecznej. Skłania nas ona z jednej strony do zaofiarowania tego mianowicie produktu, który dla innych układów wytwarzamy, z drugiej zaś do zapotrzebowania tych przedmiotów, przy których pomocy możemy naszą energię społeczną w pożądanym kierunku uzupełnić. Ściśle zatem mówiąc, należy odróżnić podaż i popyt od ich pozornych synonimów zapotrzebowania i zaoferowania. Popyt i podaż to stany psychiczne, to chęć pozbycia się lub nabycia danego towaru. A zapotrzebowanie i zaoferowanie to przybliżone ilości, w których pragnęlibyśmy towar jakiś nabyć lub sprzedać.”
Kiedy mama wysyłała mnie do sklepu, mogłem kupić dowolną ilość cukru.
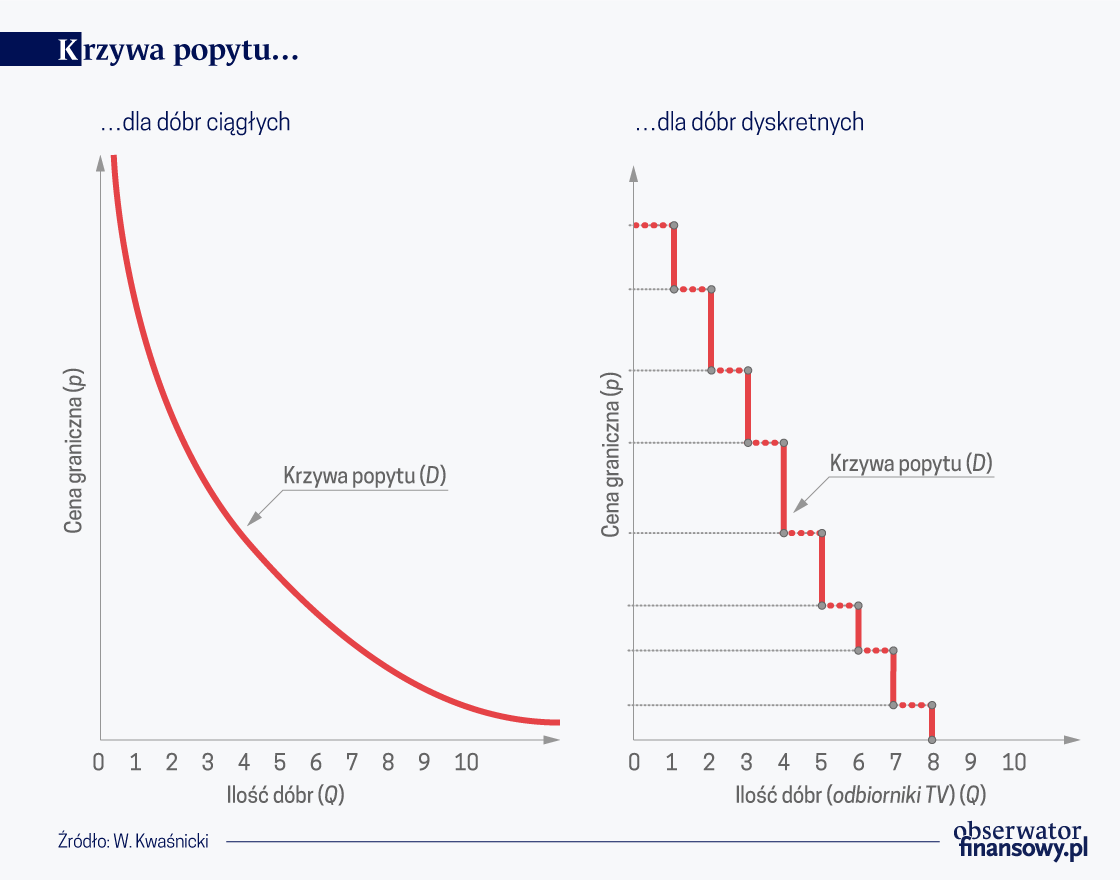
Mówiąc o krzywej popytu, czy o funkcji popytu, ekonomiści głównego nurtu (a zwłaszcza ekonomiści neoklasyczni) nie wyróżniają też dwóch typów dóbr, które nazwać można dobrami dyskretnymi i ciągłymi. Dobra dyskretne to takie, których wielkość popytu możemy wyrazić tylko jako liczby całkowite dodatnie (np. telewizory, samochody, lodówki). Nie jesteśmy w stanie kupić ćwierć lodówki, czy półtora samochodu. Natomiast w przypadku dóbr ciągłych (np. benzyna, węgiel, piasek) wielkość popytu może być wyrażona liczbą rzeczywistą dodatnią. Warto zauważyć, że w miarę rozwoju gospodarczego, wiele dóbr ciągłych stawało się dyskretnymi. Jeszcze za czasów mojego dzieciństwa, kiedy mama wysyłała mnie do sklepu, mogłem kupić dowolną ilość cukru. Na życzenie klienta, sprzedawczyni mogła odważyć np. 35 dkg cukru. Teraz możemy kupić jedynie dyskretne wartości cukru, jednostką jest kilogram (no chyba, że jest to cukier puder, lub cukier w kostkach, to wtedy jednostką może być pół kilograma).
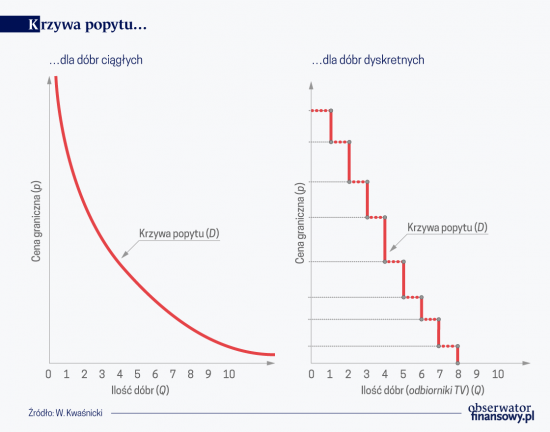
Jeśli wyróżnimy dobra dyskretne i ciągłe to też i obraz krzywej popytu powinien być różny. Najczęściej krzywa popytu przedstawiana w podręcznikach (ale też i w artykułach naukowych) jest prezentowana jako krzywa ciągła. Nawet wtedy, kiedy takim przykładowym dobrem są np. bilety do kina, czy pójście do restauracji. Tymczasem dla dóbr dyskretnych krzywa popytu powinna być krzywą schodkową.
Można twierdzić, że krzywa ciągła jest przybliżeniem krzywej schodkowej. Taką argumentację można ewentualnie przyjąć wtedy, kiedy wielkość popytu mierzymy w setkach tysięcy, czy w milionach sztuk, ale nawet wtedy należy być ostrożnym. Dosyć dziwnie wygląda np. stwierdzenie, że popyt równowagowy na samochody wynosi 121 589,7 samochodu. Czy, będąc ostrożnym, możemy wtedy zaokrąglić tę wartość do najbliższej liczby całkowitej? Tutaj rodzą się wątpliwości.
Kiedy w przypadku dóbr dyskretnych stosujemy ciągłe reprezentacje funkcji popytu i krzywej popytu, to do analizy sytuacji gospodarczej ekonomiści matematyczni stosują rachunek różniczkowy (zapożyczony od fizyków). Tymczasem powinni używać, znacznie trudniejszego w stosowaniu, rachunku różnicowego.
Co ważne, z pozoru podobne modele ciągłe i dyskretne dają często jakościowo diametralnie odmienne wyniki. Wiedzą o tym specjaliści od numerycznego rozwiązywania równań różniczkowych. Po to, by rozwiązać równanie różniczkowe na komputerze należy dokonać jego dyskretyzacji. Jeśli nie dokona się tego poprawnie, z należytą ostrożnością, to rozwiązanie uzyskane w symulacji komputerowej może się radykalnie różnić od tego, jak wygląda ono w postaci rozwiązania analitycznego danego równania różniczkowego.
Bardzo często „takie same” równania różniczkowe i różnicowe zachowują się radykalnie odmiennie, i to nie tylko w kategoriach ilościowych, ale przede wszystkim jakościowych. Podam tylko jeden przykład równana logistycznego, wykorzystywanego bardzo często do opisu procesów gospodarczych, demograficznych czy biologicznych. Może ono występować w wersji ciągłej i w wersji dyskretnej. By nie odstraszać potencjalnych czytelników nie będę przytaczał tych dosyć skomplikowanych wzorów matematycznych (więcej o tym piszę w Zauroczenie matematyką – nadinterpretacje w ekonomii głównego nurtu).
W wersji ciągłej równania logistycznego, w miarę upływu czasu, wartość zmiennej (np. wielkości produkcji, wielkości populacji biologicznej) zbliża się do tzw. wartości nasycenia (dlatego też krzywą logistyczną często nazywamy krzywą S, lub krzywą sigmoidalną). W modelu ciągłym nie mogą wystąpić drgania, fluktuacje, czy tzw. zachowanie chaotyczne.
Wersja dyskretna równania logistycznego ma podobną postać do wersji ciągłej tego równania. Jednakże rozwiązanie tego dyskretnego równania logistycznego może mieć jakościowo radykalnie odmienny charakter. Wartości zmiennej opisywanej równaniem logistycznym mogą zbliżać się powoli do wartości nasycenia (jak to było w przypadku modelu ciągłego), ale mogą wystąpić też fluktuacje, a nawet możemy obserwować zachowania chaotyczne, czy tzw. bifurkacje.
Postawię zatem retoryczne pytanie: czy stosowanie rachunku różniczkowego przez ekonomistów matematycznych do opisu zjawisk ekonomicznych, w których wartości zmiennych przyjmują wartości dyskretne, jest w pełni uzasadnione i usprawiedliwione?
Klasycznym narzędziem w ekonomii neoklasycznej jest funkcja produkcji określająca maksymalne rozmiary produkcji Q, jakie są możliwe do osiągnięcia przy różnym poziomie nakładów (czynników produkcji). Jeśli takimi podstawowymi czynnikami produkcji są kapitał (K) i praca (L), to w powszechnym użyciu jest tzw. funkcja produkcji Cobba-Douglasa, zwykle zapisywana jako:
![]()
gdzie: A – stała określająca zdolności technologiczne systemu.
Jeśli ekonomia neoklasyczna uznaje fizykę za swój metodologiczny wzorzec, to wykorzystując formalizm matematyczny do opisu zjawisk gospodarczych, ekonomiści ci powinni też przestrzegać analizy wymiarowej (czyli dokonywać tzw. rachunku mian). Problem braku analizy wymiarowej w analizie ekonomicznej przedstawił William Barnett II w swoim artykule z 2003 r., opublikowanym w Quarterly Journal of Austrian Economics. Z Krzysztofem Kostro zaprosiliśmy w 2006 r. polskich ekonomistów do zabrania głosu w tej sprawie. Podsumowanie dyskusji przedstawiłem kilka lat temu w Problemy analizy wymiarowej w ekonomii. Tutaj odwołam się jedynie do kwestii analizy wymiarowej w przypadku funkcji Cobba-Douglasa. W odróżnieniu od wszystkich dyskutantów zabierających głos w zainicjowanej przez nas dyskusji, uważam, że Barnett ma rację, ekonomiści nie stosują analizy wymiarowej (rachunku mian) i to jest ogromnym błędem metodologicznym.
Podstawowe zarzuty do powyższej postaci funkcji produkcji Cobba-Doulasa dotyczą tego, że przy dowolnych rzeczywistych wartościach a i b w wymiarach (mianach) mogą występować potęgi niewymierne oraz tego, że wartości a i b zmieniają się nie tylko w przypadku zastosowania jej do różnych produktów czy różnych krajów, ale różnią się także w zależności od tego, jaki okres do ich określania jest wybierany. Jeśli a i b zmieniają się w czasie i w zależności „od okoliczności” to stała proporcjonalności A zmienia zarówno swoja wartość jak i wymiary (miana). To tak jakby wymiar stałej grawitacji w równaniu opisującym prawo powszechnego ciążenia (zaproponowanym przez Newtona) zmieniał się w czasie i w zależności „od okoliczności”.
Co ciekawe, z tego typu problemów związanych z „rachunkiem mian” zdawali sobie sprawę Charles Wiggins Cobb i Paul Howard Douglas, „twórcy” tej postaci funkcji produkcji. Analiza ich oryginalnego artykułu z 1928 roku wyraźnie na to wskazuje. Cobb i Douglas zebrali dane statystyczne dotyczące wielkości zaangażowanego kapitału i pracy oraz wielkości produkcji w gospodarce amerykańskiej (w sektorze produkcji przemysłowej) z lat 1899-1922. Przy estymacji parametrów funkcji produkcji Cobb i Douglas nie posługiwali się wartościami bezwzględnymi, a wartościami względnymi (wskaźnikami). Wartości kapitału, pracy i produkcji w poszczególnych latach odnosili do wartości tych zmiennych w 1899 roku (przyjmując wartości tych wskaźników w tym roku jako 100).
Zatem postać funkcji produkcji stosowanej przez Cobba i Douglasa to:
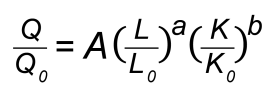
Stosując taką postać funkcji produkcji, Cobb i Douglas unikają wszelkich problemów związanych z analizą wymiarową, gdyż wszelkie używane przez nich zmienne są bezwymiarowymi wskaźnikami. Można by zatem powiedzieć, że przynajmniej w przypadku takiej postaci funkcji produkcji Cobba-Douglasa problem postawiony przez Barnetta samoistnie znika. Nie oznacza to, że postulowana przez Barnetta konieczność rygorystycznego stosowania analizy wymiarowej w ekonomii także przestaje być zasadna. Problem ten nadal istnieje i potrzeba rygorystycznego przestrzegania zasad analizy wymiarowej w ekonomii jest tak samo ważna w fizyce, jak i we wszelkich innych naukach.
To podstawowe równanie używane w ilościowej teorii pieniądza przedstawiane jest najczęściej w postaci:
![]()
gdzie: M to podaż pieniądza w gospodarce, V szybkość obiegu jednostki pieniądza w ciągu roku (której miarą może być średnia liczba transakcji obsługiwanych przez jednostkę pieniądza w ciągu roku), Y wielkość PKB, P średni poziom cen w gospodarce.
W takiej postaci równanie to nie spełnia wymogów analizy wymiarowej (rachunku mian). Lewa strona równania wyrażona jest w jednostce pieniężnej danego kraju (złoty, dolar, euro), a prawa strona wyrażona jest w jednostce pieniężnej podniesionej do kwadratu. PKB wyrażany jest w wartościach pieniężnych, P też jest wyrażone w pieniądzu (niekiedy można przeczytać, że P jest „ceną jednostki dochodu krajowego PKB” – tylko trudno jest określić co to jest ta „jednostka PKB”).
Irwing Fisher, podobnie jak Cobb i Douglas, świadomy był konieczności spełnienia wymogów analizy wymiarowej. Postać równania jaką zaproponował Fisher (1897, 1911) spełniała te warunki analizy wymiarowej (obie strony równania wyrażone są w jednostce pieniężnej: w złotych, dolarach czy euro):
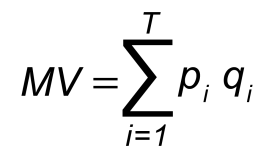
gdzie, M ilość pieniądza będącego w obiegu, V szybkość obiegu pieniądza, T liczba wszystkich transakcji dokonanych w ciągu roku, pi cena jednostki i-tego towaru lub usługi, qi ilość i-tego towaru (lub usługi). Fisher uzasadnia możliwość przekształcenia powyższej formy równania w postać uproszczoną (zagregowaną):
![]()
gdzie: P jest średnią wartością dokonywanych w ciągu roku transakcji (T podobnie jak wcześniej liczba wszystkich transakcji dokonanych w ciągu roku). Naturalnie ta nowa postać równania też spełnia warunki analizy wymiarowej.
Nie jestem zawodowym historykiem myśli ekonomicznej i trudno mi stwierdzić, kiedy nastąpiło przekształcenie oryginalnego równania Fishera w tę „postać podręcznikową”. Wiele wskazuje, że po raz pierwszy uczynił to już w 1936 roku James Angell w The Behavior of Money: Exploratory studies. Ta postać równania szybko została zaakceptowana przez szkołę keynesowską i neoklasyczną i teraz jest powszechnie używana w podręcznikach ekonomii.
W końcu lat 50. Alban William Phillips analizował dane statystyczne dotyczące rynku pracy w Wielkiej Brytanii. Dysponował danymi statystycznymi z dosyć długiego okresu 1861-1957. W tych rozważaniach zajmował się szczególnie zależnością między wielkością bezrobocia (U) a stopą zmian płac nominalnych (W). Wyniki tych badań opublikował w znanym artykule pt. Relationship between Unemployment and the Rate of Change of Money Wages in the United Kingdom 1861-1957. Racjonalnie rzecz ujmując, możemy zgodzić się z proponowaną przez Phillipsa zależnością, że czym wyższe bezrobocie tym płace szybciej maleją i odwrotnie – im bezrobocie bardziej zbliża się do zera tym szybciej rosną płace.
Niezrozumiałe jednak wydaje mi się to, co już dwa lata po publikacji Phillipsa zaproponowali Paul Samuelson i Robert Solow. W 1960 r. Samuelson i Solow opublikowali w prestiżowym American Economic Review artykuł pt. Analytical Aspects of Anti-Inflation Policy. W artykule tym dokonali reinterpretacji krzywej zaproponowanej przez Phillipsa i przedstawili ją jako zależność między wielkością bezrobocia i poziomem inflacji. Stwierdzili, że istnieje wymienność pomiędzy inflacją a bezrobociem (wysokiej inflacji towarzyszy niskie bezrobocie i odwrotnie, gdy chcielibyśmy zmniejszyć inflację, to musimy zgodzić się na to, aby wzrosło bezrobocie).
Pod rysunkiem zatytułowanym „Zmodyfikowana krzywa Phillipsa dla USA”, obrazującym zależność pomiędzy „Średnim wzrostem cen” i „Bezrobociem”, Samuelson i Solow napisali, że krzywa ta została „z grubsza oszacowano na podstawie ostatnich dwudziestu pięciu lat amerykańskich danych”. Nie pokazali tych danych i trudno jest ocenić jakość tego „oszacowania”.
Kolejne pokolenia studentów uczone są błędnej postaci krzywej Phillipsa.
Wprawdzie pod koniec swojego artykułu przedstawiają oni kilka „ostrzeżeń”, co do zasadności ich propozycji, nie przeszkodziło to jednak Paulowi Samuelssonowi już 1961 roku włączyć tak zreinterpretowaną „krzywą Phillipsa” do piątego wydania swojego podręcznika Economics. Podręcznik ten był w tamtym czasie traktowany jako wzorcowy i wielu innych autorów podręczników (jak również artykułów naukowych) dokonało tego samego w następnych latach. W ten sposób kolejne pokolenia studentów uczone są tej błędnej postaci krzywej Phillipsa, ale – co znacznie gorsze – doradzający rządom ekonomiści i politycy odpowiedzialni za regulacje gospodarcze byli (i są) przekonani, że taka krzywa może być podstawą prowadzenia polityki gospodarczej rządów. W tej zmodyfikowanej postaci „krzywa Phillipsa” weszła do standardowego zestawu „narzędzi” polityki gospodarczej keynesistów i neoklasyków.
Warto zacytować opinię Daniela Yankelowicha (teoretyka, profesora psychologii, ale także praktyka – założyciela znanej firmy badającej rynki) o nadmiernej ufności pokładanej w liczbach i liczeniu: „Krok pierwszy to zmierzyć i policzyć to, co może być łatwo zmierzone i policzone. I to jest całkiem okej. Krok drugi to pominąć to, czego nie da się zmierzyć i policzyć albo przypisać temu czemuś jakąś arbitralną wartość liczbową. To jest posunięcie sztuczne, które wprowadza nas w błąd. Krok trzeci to przyjąć, że to, co nie da się zmierzyć i policzyć, tak naprawdę nie jest zbyt ważne. To jest ślepota. Krok czwarty to stwierdzić, że to, czego się nie da zmierzyć i policzyć, właściwie nie istnieje. To samobójstwo”.